How To Find Angles Of A Trapezoid
Trapezoid
A trapezoid is a quadrilateral with one pair of parallel sides. The figure below shows a few dissimilar types of trapezoids.

Notation: Some define a trapezoid as a quadrilateral with at least ane pair of parallel sides implying that information technology could contain two pairs of parallel sides, which would go far a parallelogram. For the sake of this article, we will ascertain a trapezoid equally a quadrilateral with only i pair of parallel sides.
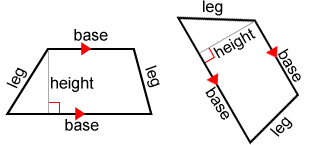
Sides of a trapezoid
The parallel sides of a trapezoid are referred to as its bases. The non-parallel sides are chosen legs. The height (or altitude) is the line segment used to measure the shortest distance betwixt the 2 bases.
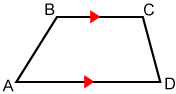
Angles of a trapezoid
In a trapezoid, the pair of angles that share a common base are chosen base angles. For the trapezoids shown in the diagram beneath, ∠A and ∠D are base angles and ∠B and ∠C are base angles. The pair of angles adjacent to a leg are supplementary: ∠A + ∠B = 180° and ∠C + ∠D = 180°.
Midsegment of a trapezoid
The midsegment of a trapezoid is a line segment connecting the midpoint of its legs. A midsegment is parallel to the bases and has a length that is one-half the sum of the two bases.
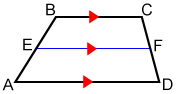
In the figure to a higher place, midsegment divides legs AB and CD in half and
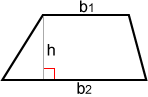
Area of a trapezoid
The surface area, A, of a trapezoid is one-half the product of the sum of its bases and its meridian.
where h is the height and bone and b2 are the base of operations lengths.
Trapezoid classifications
Trapezoids can be classified as scalene or isosceles based on the length of its legs. If the legs and base angles of a trapezoid are congruent, information technology is an isosceles trapezoid. Otherwise, it is a scalene trapezoid.
| Scalene trapezoid | Isosceles trapezoid |
|---|---|
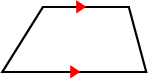 | 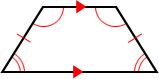 |
| Legs or base angles not congruent | Congruent legs and base angles |
Trapezoids can too be classified as right trapezoids or birdbrained trapezoids based on its angles. If ane of the legs is perpendicular to the bases, the trapezoid is a right trapezoid. Otherwise the trapezoid must incorporate two obtuse angles and is called an obtuse trapezoid.
| Right trapezoid | Obtuse trapezoid |
|---|---|
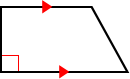 |  |
| I leg is perpendicular to the bases. | 2 angles are obtuse. |
Isosceles trapezoids
An isosceles trapezoid is a special trapezoid with congruent legs and base of operations angles. It has the following properties.
Source: https://www.math.net/trapezoid
Posted by: hernandezwinger.blogspot.com


0 Response to "How To Find Angles Of A Trapezoid"
Post a Comment